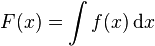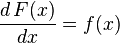Como proteger el medio ambiente

Cada día, es más inminente el deterioro del medio ambiente, por ende, es igual de considerable el deterioro de la calidad de vida de la población de todo el planeta. Integrar en las conciencias de las comunidades, el cuidado y la preservación de nuestro entorno, es imperativo, ya que es responsabilidad de todos, sin distinción.

Si bien las ciudades son centros de arte, cultura, negocios y gobierno, la expansión urbana ha alcanzado velocidades tan fulminantes que se ha visto sobrepasada la capacidad para establecer y mantener normas en relación a la seguridad ambiental sostenible, que rijan para todos los habitantes por igual y que fiscalicen el cumplimiento de éstas de manera transversal. La responsabilidad hacia el medio ambiente es un asunto intercultural, que nos ataña a todos, sin importar las diferencias que puedan existir.

Cada individuo debe, en el marco de su realidad y de sus capacidades, ser capaz de identificar las formas más accesibles para ir en resguardo del entorno común y de la mantención del medio.

El compromiso debe ser en conjunto. Cada participante de la sociedad, sin importar su estrato económico, social o cultural, puede aportar con una actitud de respeto hacia el medio ambiente, ya que con cambios pequeños pero en conjunto, la tarea de desarrollar acciones que atenúen el problema será más fácil, y así se podrá generar una sociedad con desarrollo hunazo sustentable para todos los individuos. Por otra parte, los Gobiernos y las empresas también deben asumir un rol activo a través de acciones concretas y a gran escala, ya que cuentan con las capacidades de generar información y de invertir en lograr cambios radicales que se vean reflejados en un mejor ambiente para todos.

También, es fundamental que todos tengamos conocimiento de nuestros ecosistemas y de cómo inciden nuestros actos en el desarrollo normal del medio ambiente, perjudicándolo e interviniéndolo sin captar las consecuencias. Es por ello que el mundo científico debe acercarse a la ciudadanía, ya que son ellos los más indicados para entregarnos las claves sobre cuál debe ser nuestro comportamiento, proactivo y comprometido, frente a los diversos eventos que nos muestra la naturaleza. Necesitamos que los diversos sectores, y que las personas en general, sin distinción, transformen su forma de utilizar los recursos, cambiando su quehacer diario, asumiendo responsabilidades y adoptando conciencia de que el medioambiente es un eje de desarrollo fundamental para el desarrollo del mundo, y que en la medida que se deteriora, nuestra calidad de vida también resultará afectada, y para qué decir la forma de vivir de las generaciones que están por venir.

FUENTE CON MAS INFORMACION

DISTRIBUCION BINOMIAL

Es una distribución de probabilidad discreta que mide el número de éxitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.

Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:

La distribución binomial es la base del test binomial de significación estadística.

FUENTE CON MAS INFORMACIÓN 

GUÍA DE DISTRIBUCION BINOMIAL

PROBABILIDAD

Es un método mediante el cual se obtiene la frecuencia de un suceso determinado mediante la realización de un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables. La teoría de la probabilidad se usa extensamente en áreas como la estadística, la física, la matemática, las ciencias y la filosofía para sacar conclusiones sobre la probabilidad discreta de sucesos potenciales y la mecánica subyacente discreta de sistemas complejos.

FUENTE CON MAS INFORMACIÓN 

TEXTO DE COMPLEMENTACIÓN 1 

TEXTO DE COMPLEMENTACIÓN 2

UAN

Universidad Antonio Nariño entidad privada de educación superior de Colombia

Misión: 
La misión es el motivo, propósito, fin o razón de ser de la existencia de una empresa u organización porque define:
1) lo que pretende cumplir en su entorno o sistema social en el que actúa,
2) lo que pretende hacer, y
3) el para quién lo va a hacer; y es influenciada en momentos concretos por algunos elementos como: la historia de la organización, las preferencias de la gerencia y/o de los propietarios, los factores externos o del entorno, los recursos disponibles, y sus capacidades distintivas. Complementando ésta definición, citamos un concepto de los autores Thompson y Strickland que dice: "Lo que una compañía trata de hacer en la actualidad por sus clientes a menudo se califica como la misión de la compañía. Una exposición de la misma a menudo es útil para ponderar el negocio en el cual se encuentra la compañía y las necesidades de los clientes a quienes trata de servir".

Visión: 
Para Jack Fleitman, en el mundo empresarial, la visión se define como el camino al cual se dirige la empresa a largo plazo y sirve de rumbo y aliciente para orientar las decisiones estratégicas de crecimiento junto a las de competitividad.

Según Arthur Thompson y A. J. Strickland, el simple hecho de establecer con claridad lo que está haciendo el día de hoy no dice nada del futuro de la compañía, ni incorpora el sentido de un cambio necesario y de una dirección a largo plazo. Hay un imperativo administrativo todavía mayor, el de considerar qué deberá hacer la compañía para satisfacer las necesidades de sus clientes el día de mañana y cómo deberá evolucionar la configuración de negocios para que pueda crecer y prosperar. Por consiguiente, los administradores están obligados a ver más allá del negocio actual y pensar estratégicamente en el impacto de las nuevas tecnologías, de las necesidades y expectativas cambiantes de los clientes, de la aparición de nuevas condiciones del mercado y competitivas, etc... Deben hacer algunas consideraciones fundamentales acerca de hacia dónde quieren llevar a la compañía y desarrollar una visión de la clase de empresa en la cual creen que se debe convertir.

En síntesis, la visión es una exposición clara que indica hacia dónde se dirige la empresa a largo plazo y en qué se deberá convertir, tomando en cuenta el impacto de las nuevas tecnologías, de las necesidades y expectativas cambiantes de los clientes, de la aparición de nuevas condiciones del mercado, etc.

MATERIAS QUE DICTO EN LA UAN 
- Calculo diferencial
- Calculo integral
- Calculo multivariable
- Ecuaciones diferenciales
- Matemáticas especiales
- Probabilidad y estadística
- Programación

introducción a álgebra lineal

 

Es una de las ramas de las matemáticas que estudia conceptos tales como vectores, matrices, sistemas de ecuaciones lineales y en un enfoque más formal, espacios vectoriales y sus transformaciones lineales.
Es un área activa que tiene conexiones con muchas áreas dentro y fuera de las matemáticas como análisis funcional, ecuaciones diferenciales, investigación de operaciones, gráficas por computadora, ingeniería, etc.

La historia del álgebra lineal moderna se remonta a los años de 1843 cuando William Rowan Hamilton (de quien proviene el uso del término vector) creó los cuaterniones; y de 1844 cuando Hermann Grassmann publicó su libro Die lineare Ausdehnungslehre (La teoría lineal de extensión).

FUENTE

CURSO DE VÍDEO TUTORIALES EN YOUTUBE

 

MULTIPLICCION DE MATRICES



Últimos temas Matemáticas especiales

GUÍA 4

GUÍA 5

función (Exponencial, Logaritmo, Trigonométricas, hiperbólicas, )

Función Exponencial Compleja



Función Logaritmo Complejo



Exponentes Complejos



Funciones hiperbolicas

GUÍA 3

TALLER 3

USO DE LA CALCULADORA CIENTÍFICA TI-nspire cx CAS

La familia TI-Nspire es una serie de calculadora gráfica desarrollada por Texas Instruments. Esta línea está conformada actualmente por las calculadoras TI-Nspire, TI-Nspire CX y TI-Nspire CX CAS, así como también por el Sistema TI-Nspire Navigator. Además, cuentan con un software TI-Nspire para Windows y Mac OS X. En 2010 Texas Instruments actualizó las calculadoras a la versiones Touchpad1 que vienen con el Software de TI-Nspire CAS y soporte opcional de pilas recargables. En 2011 Texas Instruments anunció dos nuevos modelos de la familia TI-Nspire: la Nspire CX2 y la TI-Nspire CX CAS3 . Las principales novedades son la pantalla en color, batería recargable y diseño delgado.

FUENTE

FUNCIONES DOMINIO LIMITES en matemáticas especiales

Solución de límites de funciones de variable compleja

GUIA 2

TALLER 2

números complejos

on una extensión de los números reales y forman el mínimo cuerpo algebraicamente cerrado que los contiene. El conjunto de los números complejos se designa como , siendo el conjunto de los reales se cumple que . Los números complejos incluyen todas las raíces de los polinomios, a diferencia de los reales. Todo número complejo puede representarse como la suma de un número real y un número imaginario (que es un múltiplo real de la unidad imaginaria, que se indica con la letra i).

FUENTE



suma y resta de complejos




 multiplicación de complejos




 Multiplicación y división de complejos

GUIA 1

TALLER 1

Temas Ecuaciones Diferenciales

ECUACIONES DIFERENCIALES EXACTAS

ejercicios resueltos 

ECUACIONES DIFERENCIALES LINEALES




ECUACIONES DIFERENCIALES HOMOGENEAS




ECUACION DIFERENCIAL DE  BERNOULLI




ley de enfriamiento de newton

Problema de mezclas - Salmuera

Vaciado de recipientes

Ecuación diferencial de un circuito RL

Curso completo Ecuaciones Diferenciales

Este es un pequeño curso sobre todos los temas de Ecuaciones Diferenciales, acontinuacion veran una serie de vídeo tutoriales.

click aqui para ver la lista de reproduccion completa en YouTube

Ecuaciónes diferenciales introduccion

Una ecuación diferencial es una ecuación en la que intervienen derivadas de una o más funciones desconocidas. Dependiendo del número de variables independientes respecto de las que se deriva, las ecuaciones diferenciales se dividen en:
Ecuaciones diferenciales ordinarias: aquellas que contienen derivadas respecto a una sola variable independiente.
Ecuaciones en derivadas parciales: aquellas que contienen derivadas respecto a dos o más variables.
Fuente de informacion



EVALUACION 1

Libros

1) TEXTO EL HOMBRE MAS RICO DE BABILONIA

METODOS DE INTEGRACION

OBJETIVOS
Al finalizar esta guía el estudiante estará en capacidad de calcular integrales definidas e indefinidas, además se tendrá como herramienta el método de sustitución que consiste en el cambio de variable para hacer más simple la integral dada y la aplicación de los teoremas fundamentales del cálculo.

INTRODUCCIÓN
Se entiende por métodos de integración cualquiera de las diferentes técnicas elementales usadas para calcular una antiderivada o integral indefinida de una función. Así, dada una función f(x), los métodos de integración son técnicas cuyo uso (usualmente combinado) permite encontrar una función F(x) tal que ,

lo cual, por el teorema fundamental del cálculo equivale a hallar una función F(x) tal que f(x) es su derivada:notas

Guia de informacion
GUIA 1

DERIVADAS

la derivada de una función es una medida de la rapidez con la que cambia el valor de dicha función matemática, según cambie el valor de su variable independiente. La derivada de una función es un concepto local, es decir, se calcula como el límite de la rapidez de cambio media de la función en un cierto intervalo, cuando el intervalo considerado para la variable independiente se toma cada vez más pequeño. Por ello se habla del valor de la derivada de una cierta función en un punto dado. En términos físicos, representa la cuantía del cambio que se produce sobre una magnitud.



GUIA 10 DERIVADAS

continuidad

una función continua es aquella para la cual, intuitivamente, para puntos cercanos del dominio se producen pequeñas variaciones en los valores de la función. Si la función no es continua, se dice que es discontinua. Generalmente una función continua es aquella cuya gráfica puede dibujarse sin levantar el lápiz del papel. La continuidad de funciones es uno de los conceptos principales de la topología. El artículo describe principalmente la continuidad de funciones reales de una variable real.



GUIA 9 CONTINUIDAD

LIMITES

Que son los limites

el límite es un concepto que describe la tendencia de una sucesión o una función, a medida que los parámetros de esa sucesión o función se acercan a determinado valor. En cálculo (especialmente en análisis real y matemático) este concepto se utiliza para definir los conceptos fundamentales de convergencia, continuidad, derivación, integración, entre otros. El concepto se puede generalizar a otros espacios topológicos, como pueden ser las redes topológicas; de la misma manera, es definido y utilizado en otras ramas de la matemática, como puede ser la teoría de categorías. Para fórmulas, el límite se utiliza usualmente de forma abreviada mediante lim como en lim(an) = a o se representa mediante la flecha (→) como en an → a.




GUIA 8 LIMITES


ejercicios limites 

FUNCIONES

FUNCION PAR E IMPAR

se puede clasificar a las funciones según su paridad. Las funciones pueden ser pares, impares o no tener paridad. Aquellas funciones que poseen paridad satisfacen una serie de relaciones particulares de simetría, con respecto a inversas aditivas. Las funciones pares e impares son usadas en muchas áreas del análisis matemático, especialmente en la teoría de las series de potencias y series de Fourier. Deben su nombre a la paridad de las potencias de las funciones monómicas que coinciden y por tanto satisfacen las condiciones de paridad. Así, la función xn es una función par si n es un entero par es o una función impar si n es un entero impar.

GUIA 7 FUNCION PAR E IMPAR, TRIGONOMETRICAS

FUNCIONES TRIGONOMETRICAS

son las funciones establecidas con el fin de extender la definición de las razones trigonométricas a todos los números reales y complejos. Las funciones trigonométricas son de gran importancia en física, astronomía, cartografía, náutica, telecomunicaciones, la representación de fenómenos periódicos, y otras muchas aplicaciones.




FUNCION EXPONENCIAL

es conocida formalmente como la función real ex, donde e es el número de Euler, aproximadamente 2.71828...; esta función tiene por dominio de definición el conjunto de los números reales, y tiene la particularidad de que su derivada es la misma función. Se denota equivalentemente como f(x)=ex o exp(x), donde e es la base de los logaritmos naturales y corresponde a la función inversa del logaritmo natural.

GUIA 7 FUNCION EXPONENCIAL

FUNCION LOGARITMICA

el logaritmo de un número —en una base de logaritmo determinada— es el exponente al cual hay que elevar la base para obtener dicho número. Por ejemplo, el logaritmo de 1000 en base 10 es 3, porque 1000 es igual a 10 a la potencia 3: 1000 = 103 = 10×10×10. De la misma manera que la operación opuesta de la suma es la resta y la de la multiplicación la división, el cálculo de logaritmos es la operación inversa a la exponencial de la base del logaritmo.

FUNCIONES A TROZOS Y MOVIMIENTOS EN EL PLANO

INTRODUCCIÓN

Es de gran utilidad que el estudiante se encuentre familiarizado con las funciones a trozos y
movimientos de las gráficas en el plano para que use estos conceptos en temas como límites y
continuidad.

OBJETIVOS
• Realizar gráficas de funciones a trozos.
• Realizar gráficas de funciones utilizando traslaciones.

METODOLOGÍA
En esta guía los estudiantes:
• Leen los conceptos, estudian los ejemplos y resuelven los ejercicios planteados.
• Asisten a las asesorías del tutor programadas por la Universidad.
• Plantean sus inquietudes al tutor a través de Chats, correo electrónico, clases virtuales.
• Reciben orientaciones del tutor de manera presencial.

LOGROS
El estudiante estará en capacidad de:
1. Trazar el gráfico de una función a trozos.
2. Dada la gráfica de una función a trozos encontrar su ecuación.
3. Dada una gráfica determinar los movimientos que se han dado en otra grafica para
obtenerla.
Dada la expresión de una función obtener su grafica a partir de movimientos en el plano

FUNCIONES A TROZOS Y MOVIMIENTOS EN EL PLANO

TALLER 6

GRAFICAS DE PARABOLAS

Lo mismo que por dos puntos del plano casi siempre pasa una recta de ecuación y=Ax+B, por tres puntos casi siempre pasa una parábola de ecuación y=Ax²+Bx+C.

El cuadro siguiente sirve para dibujar gráficas de parábolas. Instrucciones de uso:

1. pinchar los tres puntos hasta que se pongan verdes.
2. arrastrarlos a donde queramos que pase la parábola.

FUNCION CUADRATICA

COMPOSICION DE FUNCIONES

Funciones Compuestas

una función compuesta es una función formada por la composición o aplicación sucesiva de otras dos funciones. Para ello, se aplica sobre el argumento la función más próxima al mismo, y al resultado del cálculo anterior se le aplica finalmente la función restante. Usando la notación matemática, la función compuesta g ∘ f: X → Z expresa que (g ∘ f)(x) = g(f(x)) para todo x perteneciente X. A g ∘ f se le llama composición de f y g. Nótese que se nombra no siguiendo el orden de escritura, sino el orden en que se aplican las funciones a su argumento.

GUIA 5 COMPOSICION DE FUNCIONES

TALLER 5

DOMINIO Y RECORRIDO DE UNA FUNCION

INTRODUCCIÓN

En esta guía se tratan los aspectos básicos de una función, se reconoce y se hallan el dominio y el recorrido, usando el gráfico y en forma analítica.

OBJETIVOS
1- Determinar si una ecuación dada es o no una función.
2- Identificar el dominio y el recorrido (recorrido de una función).
3- Trazar gráficas de funciones.

METODOLOGÍA
En esta guía los estudiantes:
1- Leen los conceptos, estudian los ejemplos y resuelven los ejercicios planteados.
2- Asisten a las asesorías del tutor programadas por la Universidad.
3- Plantean sus inquietudes al tutor a través de Chats, correo electrónico, clases virtuales.
4- Reciben orientaciones del tutor de manera presencial.

LOGROS 
Un estudiante alcanzara sus logros si:
1. Dada una función es capaz de hallar su dominio.
2. Dada una función es capaz de hallar su recorrido (recorrido).


Recorrido de una funcion (dominio y rango)

DOMINIO Y RECORRIDO DE UNA FUNCION

TALLLER 4

CIRCUNFERENCIA Y DISTANCIA

INTRODUCCIÓN

En la siguiente guía, encontrará una serie de ejercicios que le permiten usar y afianzar los conceptos de: distancia entre dos puntos, identificar el radio y centro de un círculo a partir de su ecuación, así como identificar,la pendiente e intercepto de una recta a partir de su ecuación. Obviamente, muchos de los ejercicios requieren de manipulaciones algebraicas para poder identificar sus correspondientes elementos. Todo con el fin de, proporcionar los fundamentos matemáticos necesarios para los conceptos que se trabajan en talleres y asignaturas posteriores.

OBJETIVOS
• Hallar la distancia entre puntos del plano.
• Hallar la ecuación de una circunferencia y dada la ecuación de la circunferencia hallar el centro y el radio.
• Hallar la ecuación de una recta y trazar su gráfica.

METODOLOGÍA
En esta guía los estudiantes:
• Leen los conceptos, estudian los ejemplos y resuelven los ejercicios planteados.
• Asisten a las asesorías del tutor programadas por la Universidad.
• Plantean sus inquietudes al tutor a través de Chats, correo electrónico, clases virtuales.
• Reciben orientaciones del tutor de manera presencial.

LOGROS
El estudiante estará en capacidad de:
1. Dados 2 puntos en el plano, hallar su distancia.
2. Determinar la ecuación de una circunferencia dados su centro y radio.
3. Dada la ecuación de una circunferencia, encuentra su centro y su radio.

Distancias iguales a un punto exterior a una circunferencia



Distancia de una tangente a un círculo

GUIA 3 CIRCUNFERENCIA Y DISTANCIA

EJERCICIOS DE CIRCUNFERENCIA

NUMEROS REALES E INECUACIONES

INTRODUCCIÓN 

En esta guía se exploran algunas propiedades fundamentales de los números reales, las
cuales se usan para determinar la solución de inecuaciones y de ecuaciones que
involucran valor absoluto.

OBJETIVOS 
• Reconocer el conjunto de los números reales.
• Estudiar las propiedades en R y aplicarlas en la solución de ejercicios y
problemas.
• Resolver inecuaciones de números reales con y sin valor absoluto.

METODOLOGÍA 
En esta guía los estudiantes:
• Leen los conceptos, estudian los ejemplos y resuelven los ejercicios planteados.
• Asisten a las asesorías del tutor programadas por la Universidad.
• Plantean sus inquietudes al tutor a través de Chats, correo electrónico, clases
virtuales.
• Reciben orientaciones del tutor de manera presencial.

LOGROS 
Un estudiante habrá alcanzado sus logros en el tema si:
• Identifica cada uno de los conjuntos numéricos.
• Determina correctamente el intervalo solución de una inecuación


NÚMEROS REALES



INECUACIONES

GUIA 2 NUMEROS REALES E INECUACIONES

EXPRESIONES ALGEBRAICAS

Una expresión algebraica es una combinación de constantes y variables de números reales
ligadas mediante las operaciones básicas: suma, resta, producto, potenciación y radicación.

GUIA 1 EXPRESIONES ALGEBRAICAS

entrada de prueba

en este vídeo tutorial se podrán dar una idea de como empezar su proceso de aprendizaje de calculo integral, espero lo disfruten y los beneficie :)